5. Cutting data of interest from SQW files and objects

The sqw object is the main object Horace uses. It contains complete information about the results of a neutron experiment. This includes information about each neutron “event” registered in the experiment. We refer to this information as the “pixels”, which make up the majority of the sqw ‘s memory usage. Another key part of the sqw is a 0- to 4-dimensional histogram (binning) of the “pixels”, which we call the “image”. Most often this binning is done in reciprocal space (hkl-dE). This carries only limited information about the original experiment, i.e. only the average neutron intensity in each of the reciprocal space bins. The “image” is the main part of Horace’s dnd along with some meta-information for displaying and analysing it.

Note

For the differences between dnd and sqw objects see: here

Generally, rather than attempting to deal with the full experimental data, a user works with smaller objects, extracted from the full dataset using cut. This is for multiple reasons including:

• The 4-dimensional dataset is impossible to visualise, as only 3-d (through slice-o-matic), 2-d and 1-d cuts can be easily represented.

• The entire dataset is often too large to fit in the memory of most computers.

Note

The “pixels” can be mapped from their 4-D spatial coordinates into the “image” by a transformation determined by the projection (below). cut computes the bin to which “pixel” contributes, removing those pixels which do not contribute from the resulting sqw.

It also sorts the pixels according to which bins they are in, in accordance with the bin’s grid-index. This improves the speed with which they can be processed.

5.1. cut

cut takes a (or multiple) section(s) of data from an sqw or dnd object or file, discards the pixels which lie outside of the binning regions (described below), extracts contributing pixels and accumulates their signal and variance into a histogram (the “image” or dnd, which may be independent if requested or be part of the target sqw). It can return an object or file depending on the parameters given.

cut can produce objects of the same or reduced size and dimensions. The result of a cut is itself an sqw or dnd object which can be further plotted, manipulated, etc.

Note

If the resulting object is estimated by Horace to be too big to fit in memory, it will be saved to disc, but will appear mostly indistinguishable from a memory-backed sqw object, supporting most operations. We call this a “file-backed sqw” (for more detail see: File- and memory-backed cuts). When the manual refers to an sqw object both “file-backed” and “memory-backed” are included.

Warning

File-backed objects may be significantly slower to operate on than memory backed ones.

The inputs are as follows:

my_cut = cut(data_source[, proj], p1_bin, p2_bin, p3_bin, p4_bin[, '-nopix'][, sym][, filename])

where:

• data_source is either a string giving the full filename (including path) of an input sqw file or a variable containing a sqw object.

• proj defines the axes and origin of the cut including the shape of the region to extract and the representation in the resulting histogram.

• pN_bin describe the histogram bins to capture the data.

There are also several extra optional arguments which are:

• -nopix remove the “pixels” from the resulting object returning just a dnd object, i.e. binned data (the “image”). This option is faster and the resulting object requires less memory, but is also more restricted in what you can do with the result.

• sym cell array of symmetry operations. For a full description of usage, see here.

• filename - if provided, uses file-backed algorithms to write the resulting object directly to a file named filename and return a file-backed sqw.

Warning

If cut is called without a return argument, the filename option is mandatory.

5.1.1. Data Source

data_source in cut is either a string giving the full filename (including path) of the input .sqw file or just the variable containing an sqw or dnd object stored in memory from which the pixels will be taken.

Warning

By convention both sqw and dnd objects use the .sqw suffix when stored to disc. It is advisable to name the file appropriately to distinguish the types stored inside, e.g. MnO2_sqw.sqw, MnO2_d2d.sqw.

5.1.2. Projection (proj)

The projection defines the coordinate system and thus the meaning of the Binning arguments and the presentation of the data.

proj should be a projection type such as line_proj, sphere_proj, etc. which contains information about the desired coordinate system representation.

Note

To take a cut from an existing sqw or dnd object while retaining the existing projection, provide an empty proj argument:

w1 = cut(w, [], [lo1, hi1], [lo2, hi2], ...)

Different projections are covered in the Projection in more detail section below.

Note

Changing projection does not change the underlying pixels, merely its representation (binning) in the image and how thus it appears when plotted.

It does, however, affect which pixels are selected and which are discarded when making a cut.

5.1.3. Binning arguments

The binning arguments (p1_bin, p2_bin, p3_bin and p4_bin) specify the binning / integration ranges for the Q & Energy axes in the target projection’s coordinate system (c.f. Projection in more detail and Auto-binning algorithm).

Each can independently have one of four different forms below.

Warning

The meaning of the first, second, third, etc. component in pN_bin changes between each form. Ensure that you have the correct value in each component to ensure your cut is what you expect.

• [] Automatic binning arguments. Empty brackets indicate that the auto-binning algorithm will be used by cut to determine the bounds. The new axis bounds are calculated such that they encompass the maximal extents of the data along the given projection axis.

  The step size is taken to be the step size of the corresponding axis in the source image.

  Note

  The auto-binning algorithm is described in more detail below.

• [step] Automatic binning calculations with binning step size. A single (scalar) number defines a plot axis. The bin width will be equal to the number you specify. The lower and upper limits will be determined by the auto-binning algorithm, as above.

Note

A value of [0] is equivalent to [] using the bin size of the corresponding axis in the source image.

• [lo,hi] Integration axis in binning direction. A vector with two components defines integration axis. The signal will be integrated over that axis between limits specified by the two components of the vector.

Warning

A two-component binning axis defines the integration region between bin edges. For example, fourth binning range [-1 1] will capture pixels with energy transfer from -1 to 1 inclusive.

• [lower,step,upper] Plot axis in binning direction. A three-component binning axis specifies plot axis. The first lower and the last upper components specifying the centres of the first and the last bins of the data to be cut. The middle component specifies the bin width.

Note

If step is 0, the step is taken from the source binning axes.

Warning

A three-component binning axis defines the integration region by bin centres, i.e. the limits of the data to be cut lie between min = lower-step/2 and max = upper+step/2, including min/max values. For example, [-1 1 1] will define image range from -1.5 to 1.5 inclusive.

• [lower, separation, upper, cut_width] A vector with four components defines multiple integration axes with multiple integration limits in the selected direction.

  These components are:

  • lower Position of the lowest cut bin-centre.

  • separation Distance between cut bin-centres.

  • upper Approximate (see below) position of highest cut bin-centre

  • cut_width Width of each cut, centred on each bin-centre, thus extending one half-width in both directions

  The number of cuts produced will be one more than the number of separation-sized steps between lower and upper.

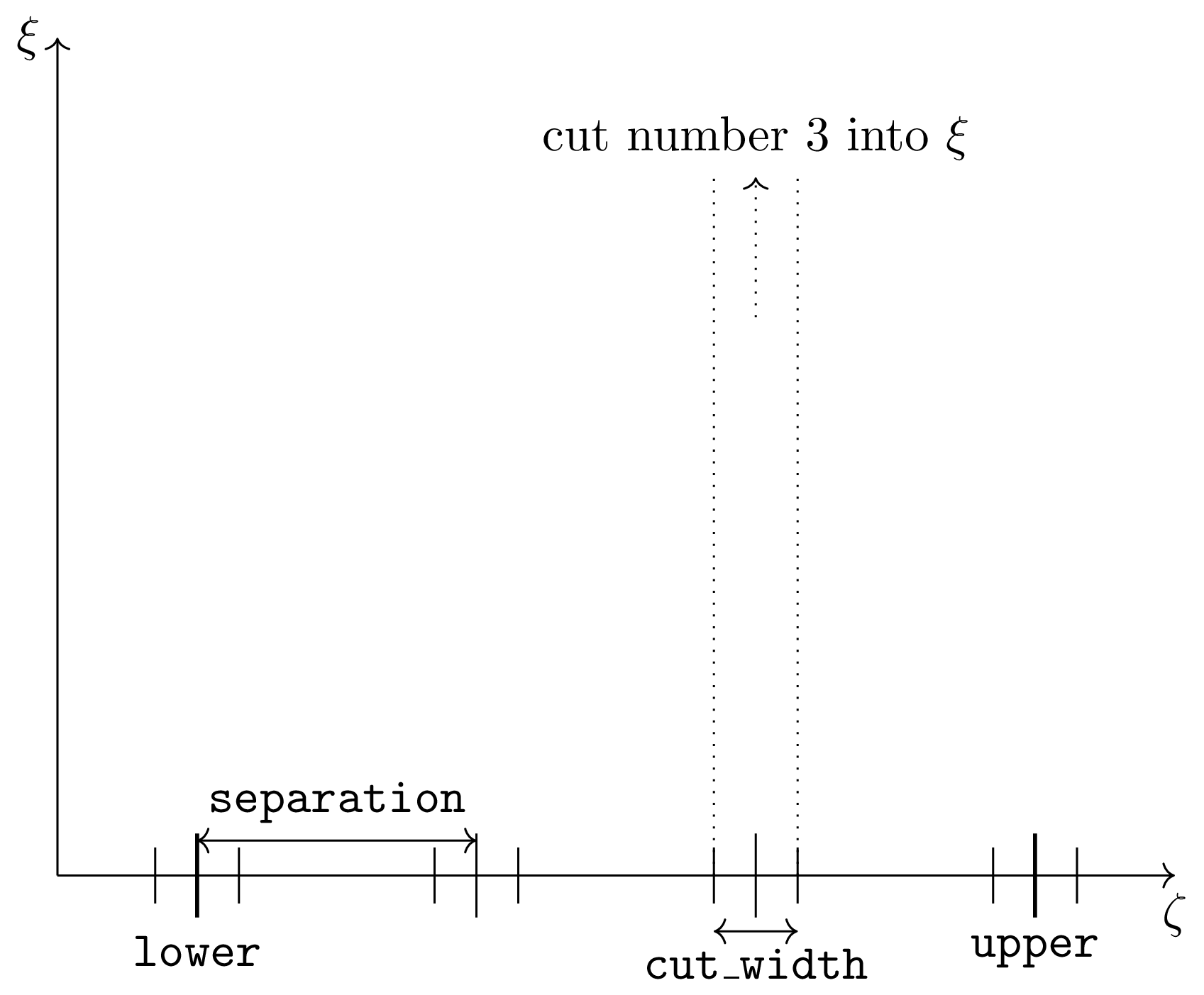
Diagram showing the relationship between the 4 binning parameters and their meaning in the context of a cut, where: lower = 1, upper = 7, separation = 2 and cut_width = 0.6, i.e [1, 2, 7, 0.6]. \(\zeta\) and \(\xi\) are arbitrary axes where \(\zeta\) is the specified axis. This will produce 4 cut objects around 1, 3, 5 and 7.

Warning

upper will be automatically increased such that separation evenly divides upper - lower. For example, [106, 4, 113, 2] defines the integration ranges for three cuts, the first cut integrates the axis over 105-107, the second over 109-111 and the third 113-115.

5.1.4. File- and memory-backed cuts

cut generally tries to return its result in memory. However, if the resulting object is sufficiently large (the threshold of which is the product of mem_chunk_size and fb_scale_factor defined in the hor_config class), the object is written to a temporary file and will be “file-backed”.

See Changing Horace settings for more information about hor_config, configuring Horace and changing the limits when object may become filebacked.

Note

The file being temporary means that it will be deleted when the sqw object backed by this file is deleted.

If the filename argument is provided to cut, the object will always saved to a file with this name and the returned object will be backed by this file. This file will not be a temporary file.

Warning

If an sqw object is backed by a temporary file, the object and its descendants (through subsequent operations) will all be temporary.

To ensure an sqw is kept, you can save this object to a file permanently.

Note

Operations with file-backed objects are substantially slower then memory-backed objects.

This is because the objects themselves are usually bigger, and because reading data from disc is around three orders of magnitude slower than from memory.

5.1.5. Projection in more detail

As mentioned in Projection (proj), the proj argument defines the coordinate system of the histogrammed image.

Warning

Horace, prior to version 4.0.0, used a structure with fields u, v, … or else a projaxes object, to define the image coordinate system. This has been replaced by the line_proj. You can still call cut with these structures, however, it will issue a warning and construct a line_proj internally.

5.1.5.1. Lattice based projections (line_proj)

The most common type of projection for single-crystal experiments is the line_proj which defines a (usually orthogonal, but not necessarily) system of linear coordinates from a set of basis vectors.

The complete signature for line_proj is:

proj = line_proj(u, v[,[],w][, nonorthogonal][, type][, alatt, angdeg][, offset][, label][, title][, lab1][, lab2][, lab3][, lab4]);

Where:

• u 3-vector in reciprocal space \((h,k,l)\) specifying first viewing axis.

• v 3-vector in reciprocal space \((h,k,l)\) in the plane of the second viewing axis.

• w 3-vector in reciprocal space \((h,k,l)\) of the third viewing axis. If left empty ([]) will default to \(\vec{w} = \frac{\vec{u}}{|u|} \times \frac{\vec{v}}{|v|}\).

Note

The first viewing axis is strictly defined to be u. The second viewing axis is constructed by default to be in the plane of u and v and perpendicular to u. The third viewing axis is, by default, defined as the cross product of the first two (\(u \times{} v\)).

The fourth viewing axis is always energy and cannot be modified.

Warning

None of these vectors can be collinear. An error will be thrown in this case.

Note

The u and v of a line_proj are distinct from the vectors u and v that are specified in gen_sqw, which describe how the crystal is oriented with respect to the spectrometer and are determined by the physical orientation of your sample.

Note

u and v are defined in the reciprocal lattice basis so if the crystal axes are not orthogonal, they are not necessarily orthogonal in reciprocal space.

E.g.:

angdeg % => [60 60 90]
proj = line_proj([1 0 0], [0 1 0]);

such that u = \([1,0,0]\) and v = \([0,1,0]\). The reciprocal space projection will actually be skewed according to angdeg.

• nonorthogonal Whether lattice vectors are allowed to be non-orthogonal

Note

If you don’t specify nonorthogonal, or set it to false, you will get orthogonal axes defined by u and v normal to u and u \(\times\) v. Setting nonorthogonal to true forces the axes to be exactly the ones you define, even if they are not orthogonal in the crystal lattice basis.

Warning

Any plots produced using a non-orthogonal basis will plot them as though the basis vectors are orthogonal, so features may be distorted (see below) .

• type Three character string denoting the the projection normalization of each of the three Q-axes, one character for each axis, e.g. 'aaa', 'rrr', 'ppp'.

  There are 3 possible options for each element of type:

  1. 'a' Inverse angstroms

  2. 'r' Reciprocal lattice units (r.l.u.) which normalises so that the maximum of \(|h|\), \(|k|\) and \(|l|\) is unity.

  3. 'p' Preserve the values of u and v

  For example, if we wanted the first two Q-components to be in r.l.u. and the third to be in inverse Angstroms we would have type = 'rra'.

• alatt 3-vector of lattice parameters.

• angdeg 3-vector of lattice angles in degrees.

Note

In general, you should not need to define alatt or angdeg when doing a cut. They are taken from the sqw object during a cut and your settings will be overridden. However, there are cases where a projection object may need to be reused elsewhere.

• offset 3-vector in \((h,k,l)\) or 4-vector in \((h,k,l,e)\) defining the origin of the projection coordinate system. For example you may wish to make the origin of all your plots \([2,1,0]\), in which case set offset = [2,1,0].

• label 4-element cell-array of captions for axes of plots.

• title Plot title for cut result.

• lab[1-4] Individual components label (for historical reasons).

Note

If you do not provide any arguments to line_proj, by default it will build a line_proj with u=[1,0,0] and v=[0,1,0].

>> line_proj()

ans =

  line_proj with properties:

                u: [1 0 0]
                v: [0 1 0]
                w: []
             type: 'ppr'
    nonorthogonal: 0
            alatt: []
           angdeg: []
           offset: [0 0 0 0]
            label: {'\zeta'  '\xi'  '\eta'  'E'}
            title: ''

Note

line_proj accepts arguments both positionally and as key-value pairs e.g.

>> proj = line_proj([0, 1, 0], [0, 0, 1], 'type', 'aaa', 'title', 'My linear cut')

line_proj with properties:

             u: [0 1 0]
             v: [0 0 1]
             w: []
          type: 'aaa'
 nonorthogonal: 0
        offset: [0 0 0 0]
         label: {'\zeta'  '\xi'  '\eta'  'E'}
         title: 'My linear cut'

However, it is advised that besides u and v arguments are passed as key-value pairs.

Alternatively you may define some parameters in the constructor, and define others later by setting their properties:

proj = line_proj([0,1,0],[0,0,1]);
proj.type = 'aaa';
proj.title = 'My linear cut';

Both forms result in the same object

5.1.5.1.1. Non-orthogonal axes

You may choose to use non-orthogonal axes (c.f. here), e.g.:

proj = line_proj([1 0 0], [0 1 0], [0 0 1], 'nonorthogonal', true);

Below is an example:

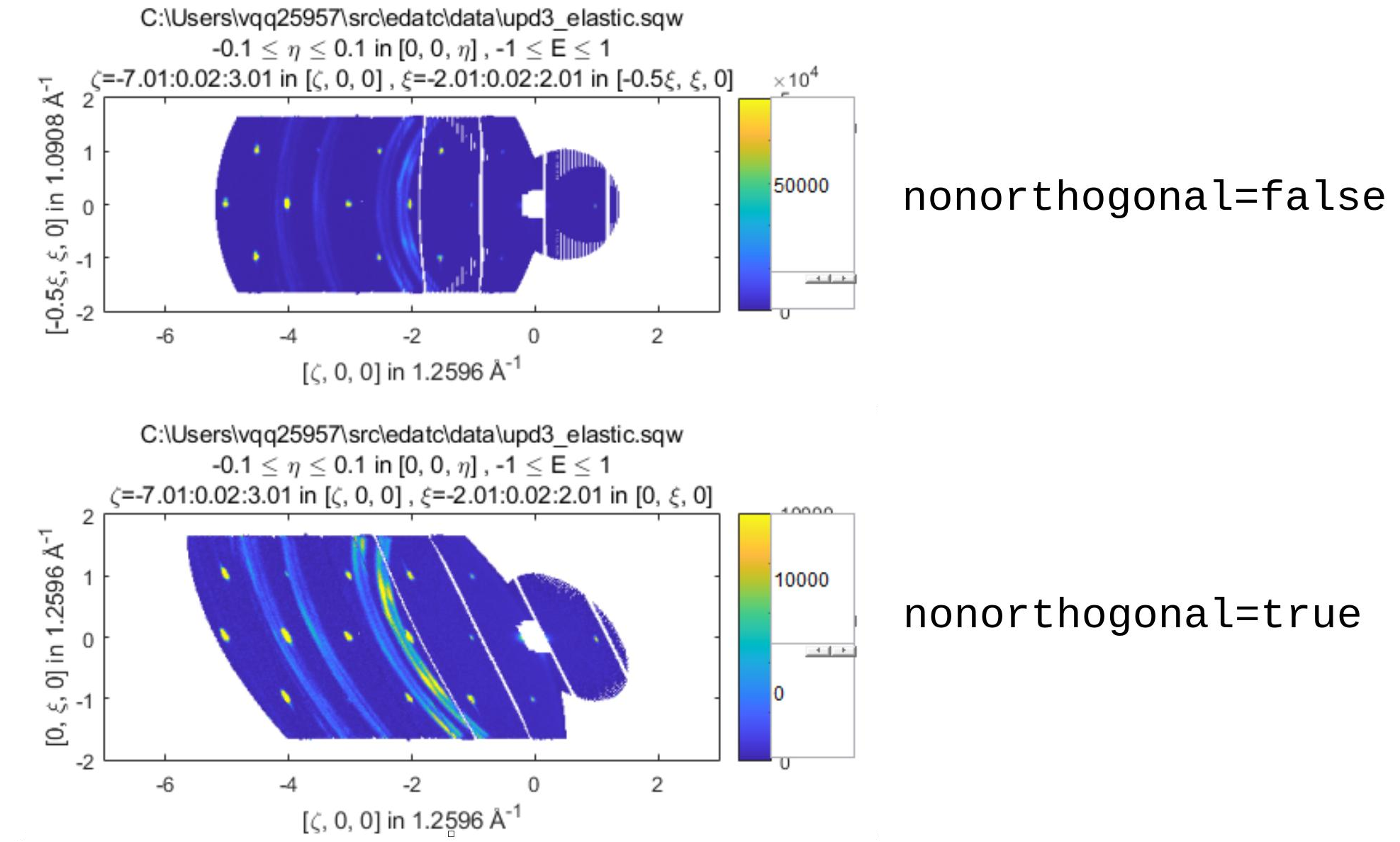
Plot to show the difference between nonorthogonal=false and nonorthogonal=true with a hexagonal material (\(\textrm{UPd}_3\)) where angdeg=[90,90,120].

We can see that for the nonorthogonal=false case, the image clearly shows the hexagonal symmetry and circular powder rings, but the axes being \([\zeta,0,0]\) and \([-0.5\xi,\xi,0]\) even in this simple case makes computing where points lie in \(hkl\) trickier.

Where we have nonorthogonal=true, this makes it easier to calculate the location of points in \(hkl\) (the Bragg peaks align in a square pattern and the axes are simply \([\zeta,0,0]\) and \([\xi,0,0]\)), but distorts the image (note the powder rings which should be circular).

5.1.5.1.2. line_proj 2D cut examples: Fe Scattering Function

Note

This dataset is available as part of the Horace source on Github.

The iron crystal has been aligned along the \([1,0,0]\) axis.

To reproduce the example below, a cut is first made along the \([0,1,0]\) and \([0,0,1]\) directions:

data_source = 'Fe_ei401.sqw';
proj = line_proj([0, 1, 0], [0, 0, 1], 'type', 'aaa');
w2 = cut(data_source, proj, [-4.5, 0.1, 14.5], [-5, 0.1, 5], [-0.1, 0.1], [-10, 10]);
plot(w2);

Note

You do not need to provide a lattice for the projection as cut will use the lattice parameters from the sqw object.

The code produces:

MAPS Fe data; reciprocal space covered by MAPS for an iron sample with incident neutron energy of 401meV.

The cut with the same parameters as above at higher energy transfer

w2 = cut(data_source, proj, [-4.5, 0.1, 14.5], [-5, 0.1, 5], [-0.1, 0.1], [50, 60]);
plot(w2);

shows clear spin waves:

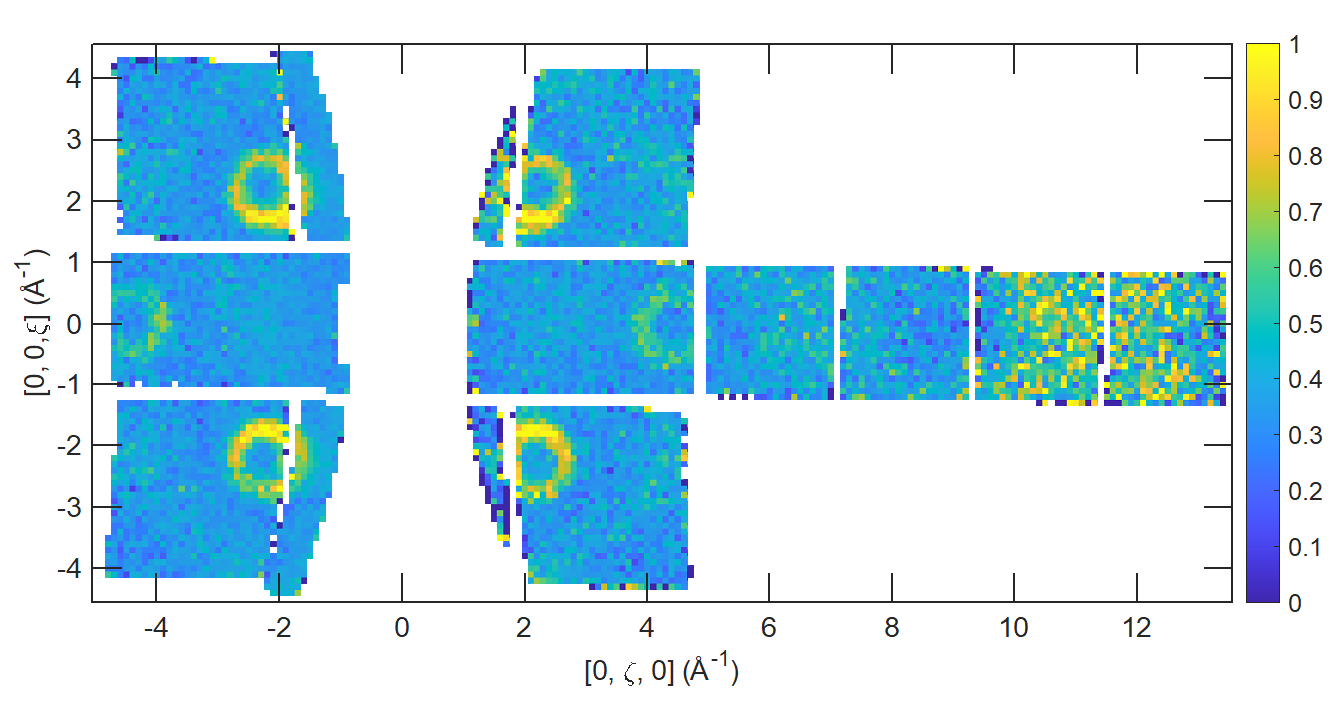
MAPS Fe Data; reciprocal space covered by MAPS for an iron sample with incident neutron energy of 401meV. Energies integrated between [50, 60].

5.1.5.1.3. line_proj 1D cut example

It is simple to take a 1-d cut by integrating over all but one axis. The example cut generated by the code below shows a cut along the \([1,1,0]\) direction (note the projection’s u & v), i.e. the diagonal of the figure above.

data_source = 'Fe_ei401.sqw';
proj = line_proj([1, 1, 0], [-1, 1, 0], 'offset', [-1, 1, 0]);
w1 = cut(data_source, proj, [-5, 0.1, 5], [-0.1, 0.1], [-0.1, 0.1], [-50, 60]);
plot(w1);

This shows the intensity of the spin wave:

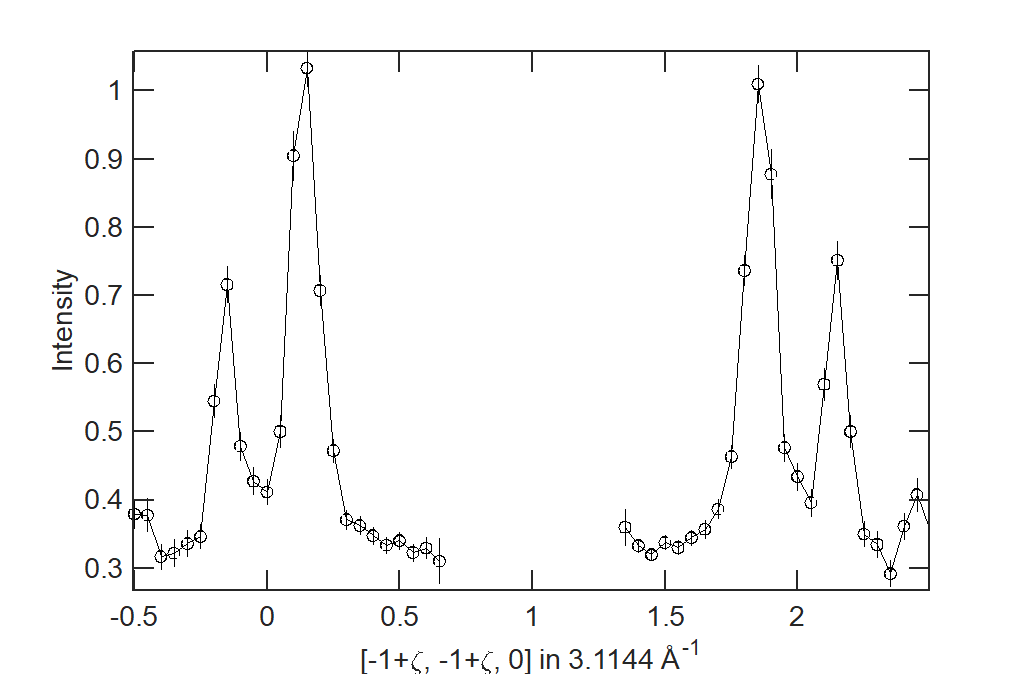
MAPS Fe Data; 1D cut along the diagonal of the 2D image above.

5.1.5.2. Spherical Projections

In order to construct a spherical projection (i.e. a projection in \(|\textbf{Q}|\), \(\theta\) (polar angle), \(\phi\) (azimuthal angle), \(E\)) we create a projection in an analogous way to the line_proj, but using the sphere_proj function.

The complete signature for sphere_proj is:

proj = sphere_proj([u][, v][, type][, alatt][, angdeg][, offset][, label][, title][, lab1][, lab2][, lab3][, lab4])

where:

• u The vector \(\vec{u}\) is the reciprocal space vector defining the polar-axis \(\vec{e_z}\) of the spherical coordinate system from which \(\theta\) is measured.

  See the diagram below for details.

• v The vector \(\vec{v}\) is the reciprocal space vector which defines the second component of the \(u\)-\(v\) plane from which \(\phi\) is measured.

  See the diagram below for details.

Note

The reciprocal space vectors \(u\)-\(v\) are not necessarily orthogonal so the actual axis \(\vec{e_x}\) from which \(\phi\) is measured lies in the plane defined by \(u\)-\(v\) vectors and is orthogonal to \(\vec{e_z}\).

Note

By default a sphere_proj will define its principal axes \(u\) and \(v\) along the \(hkl\) directions \([1,0,0]\) and \([0,1,0]\) respectively.

• type Three character string denoting the the projection normalization of each dimension, one character for each directions, e.g. 'add', 'hrr', 'adr'.

  There are 6 possible options defining scale for the value of the momentum transfer:

  1. 'a' \(|Q|\) is measured in inverse angstroms.

  2. 'r' Reciprocal lattice units (r.l.u.) which normalises vector \(\vec{Q}\) so that the scale is the maximal value of the \(\vec{u}\) projection to the unit vectors directed along the reciprocal lattice vectors.

  3. 'p' The scale is the length of the vector \(\vec{u}\)

  4. 'h' The scale is the length of \(a^{*}\), the first vector of reciprocal lattice.

  5. 'k' The scale is the length of \(b^{*}\), the second vector of reciprocal lattice.

  6. 'l' The scale is the length of \(c^{*}\), the third vector of reciprocal lattice.

  There are 2 possible options for the second and third (angular) components of type:

  1. 'd' Degrees

  2. 'r' Radians

  For example, if we wanted the \(|\textbf{Q}|\)-component to be in inverse angstroms and the angles in degrees we would have type = 'add'.

• alatt 3-vector of lattice parameters.

• angdeg 3-vector of lattice angles in degrees.

Note

when cutting, you should not need to define alatt or angdeg; by default they will be taken from the sqw object during a cut and your setting will be overwritten. However, there are cases where a projection object may need to be reused elsewhere.

• offset 3-vector in \((h,k,l)\) or 4-vector in \((h,k,l,e)\) defining the origin of the projection coordinate system.

• label, etc. See description for plot arguments above.

Note

If you do not provide any arguments to sphere_proj, by default it will build a sphere_proj with u=[1,0,0], v=[0,1,0], type='add' and offset=[0,0,0,0].

sp_pr = sphere_proj()

sp_pr =
   sphere_proj with properties:
          u: [1 0 0]
          v: [0 1 0]
       type: 'pdd'
      alatt: []
     angdeg: []
     offset: [0 0 0 0]
      label: {'|Q|'  '\theta'  '\phi'  'En'}
      title: ''

Note

Like line_proj, sphere_proj can be defined using positional or keyword arguments. However the same recommendation applies that positionals should only be used to define u and v.

A sphere_proj defines a coordinate system which represents momentum transfer vector \(\vec{Q}\) in spherical coordinates. offset defines the zero point of the coordinate system. If offset is zero, \(\vec{Q}\) is the vector of momentum transfer from the neutron to the magnetic or phononic excitations as measured in the experiment. The energy transfer coordinate for sphere_proj is the same as in linear coordinates.

Because the reciprocal lattice may be non-orthogonal (depending on the sample), we follow common crystallography practice and introduce an auxiliary orthogonal coordinate system defined below. This serves as the basis for calculating spherical coordinates. The basis vector \(\vec{e_z}\) is a unit vector parallel to \(\vec{u}\). The basis vector \(\vec{e_x}\) is a unit vector orthogonal to \(\vec{e_z}\) which lies in the plane defined by \(\vec{u}\) and \(\vec{v}\) (see spherical coordinates below).

Note

When the crystal lattice is orthogonal, the vector \(\vec{e_z}\) is parallel to \(\vec{u}\) and vector \(\vec{e_x}\) is parallel to \(\vec{v}\).

Then sphere_proj coordinates are:

• \(|\textbf{Q}|\) – The radius from the origin (offset) in \(hkl\)

• \(\theta\) – The angle measured from \(\vec{e_z}\) to the vector (\(\vec{Q}\)), i.e. \(0^{\circ}\) is parallel to \(\vec{e_z}\) and \(90^{\circ}\) is perpendicular to \(\vec{u}\).

• \(\phi\) – The angle measured between the vector \(\vec{Q_\perp}=\vec{Q}-\vec{e_z}(\vec{e_z}\cdot \vec{Q})\) and the plane \(\vec{u}\)-\(\vec{v}\), i.e. vector \(\vec{Q_\perp}\) with \(\phi = 0^{\circ}\) lies in the \(\vec{u}\)-\(\vec{v}\) plane and vector \(\vec{Q_\perp}\) with \(\phi = 90^{\circ}\) is normal to \(\vec{u}\)-\(\vec{v}\) plane. (parallel to \(\vec{e_y}\))

• \(E\) – The energy transfer as defined in line_proj

Note

• \(\theta\) lies in the range between \(0^{\circ}\) and \(180^{\circ}\).

• \(\phi\) lies in the range between \(-180^{\circ}\) and \(180^{\circ}\).

Where the type of an angular axis is r these values are the equivalent in radians.

Spherical coordinate system used by sphere_proj

An alternative description of the spherical coordinate system may be found on MATLAB help pages. Horace uses MATLAB methods cart2sph and sph2cart to convert an array of vectors expressed in Cartesian coordinate system to spherical coordinate system and back. The formulas, used by these methods together with the image of the used coordinate system is provided on MATLAB “cart2sph” help pages. MATLAB uses elevation angle which is related to \(\theta\) angle used by Horace by relation:

\(\theta = 90-elevation\)

azimuth angle form MATLAB help pages is equivalent to Horace \(\phi\) angle.

When it comes to cutting and plotting, we can use a sphere_proj in exactly the same way as we would a line_proj, but with one key difference. The binning arguments of cut no longer refer to \(h,k,l,E\), but to \(|\textbf{Q}|\), \(\theta\), \(\phi\), \(E\).

sp_cut = cut(w, sp_proj, Q, theta, phi, e, ...);

Warning

The form of the arguments to cut is still the same (see: Binning arguments). However:

• \(|\textbf{Q}|\) runs between \([0, \infty)\)

• \(\theta\) runs between \([0, 180]\)

• \(\phi\) runs between \([-180, 180]\)

Attempting to specify binning outside of these ranges will fail.

Where the type of an angular axis is r these values are the equivalent in radians.

5.1.5.2.1. sphere_proj 2D and 1D cuts examples:

Integrating over the angular terms of a spherical projection of a single crystal dataset will give an approximation of a powder average of the sample. Integrating over the angular terms for a powder sample is a valid powder averaging.

Note

This is because (except for low scattering angles) the detectors do not cover the full \(4\pi\) solid angular range. Thus regions without detector coverage will not be sampled by the angular spherical integration.

In contrast for a true powder sample, there will be crystal grains with the correct orientation to be detected even by the limited detector coverage.

At low scattering angles (below approximately 30 degrees on LET), the detectors do cover the full angular range so the angular integration of a single crystal dataset will give a valid powder average.

These effects are important to bear in mind when modelling the scattering - e.g. for a single crystal dataset it is best to model it as a single crystal and then let Horace perform the angular integration, rather than treating it as powder data.

The following is an example using the same data as above.

data_source = 'Fe_ei401.sqw';
sp_proj = sphere_proj([1,1,0]);
s2 = cut(data_source, sp_proj, [0, 0.02, 4.5], [0, 180], [-180, 180], [-10, 4, 400]);
plot(s2);

Note

Binning ranges are specified in the target coordinate system.

This script produces the following plot:

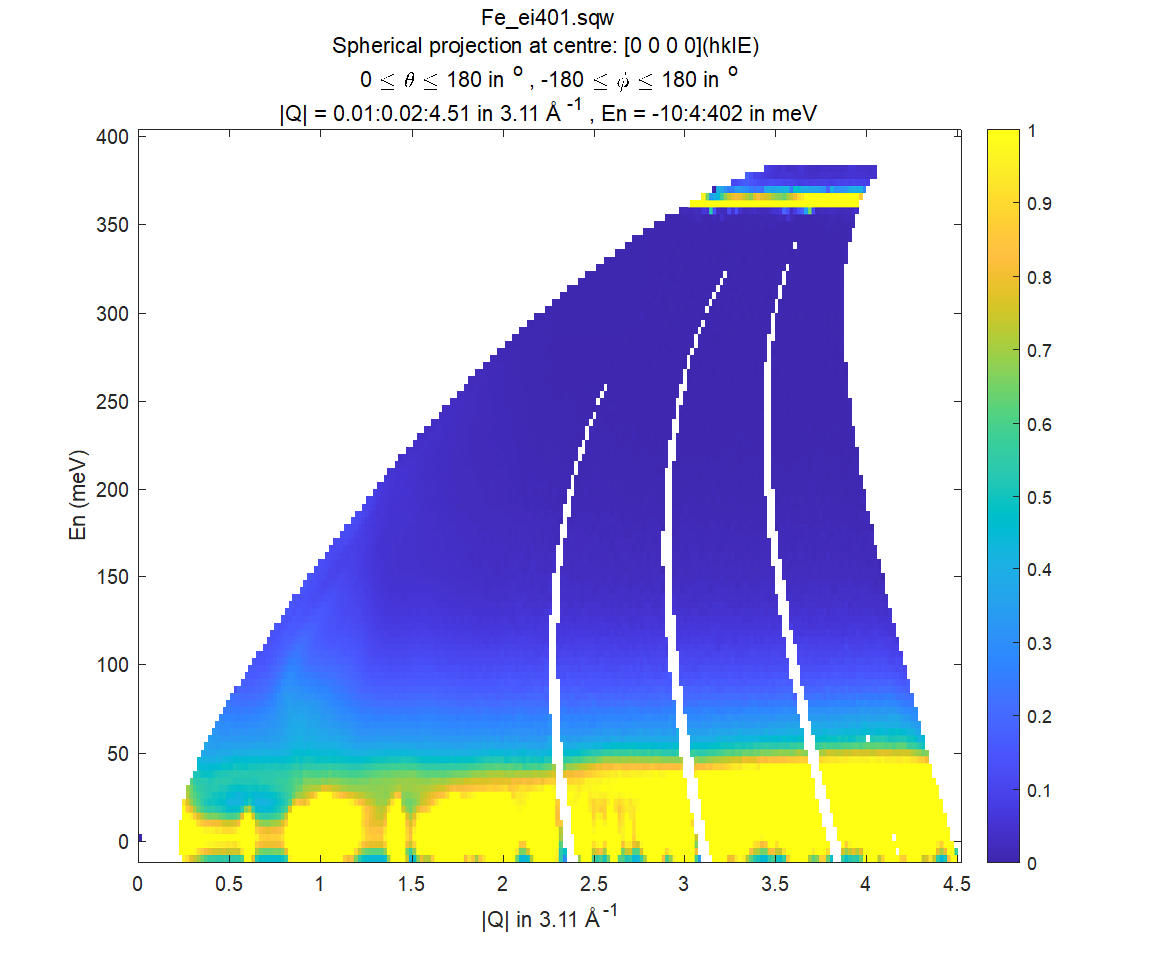
MAPS Fe data; Powder averaged scattering from iron with an incident energy of 401meV. Note integrated spin-waves at \([1,1,0]\) locations, i.e. \(|Q|=1\ in\ |[1,1,0]*a^{*}|\), \(a^{*}=2.22Å^{-1}\)

Note

By default, energy transfer is expressed in meV, momentum transfer \(\left|Q\right|\) in \(rlu\), scaled to the length of \(\vec{u}\)-vector and angles in degrees (\(^\circ\)).

This figure shows that the energies of phonon excitations are located under 50meV, some magnetic scattering is observable at \(|Q| < 5Å^{-1}\) and the spin waves are suppressed by the magnetic form factor.

A spherical projection allows us to investigate the details of a particular spin wave, e.g. around the scattering point \([0,-1,1]\).

data_source = 'Fe_ei401.sqw';
sp_proj = sphere_proj('type','add');
sp_proj.offset  = [0, -1, 1];
s2 = cut(data_source, sp_proj, [0, 0.1, 2], [80, 90], [-180, 4, 180], [50, 60]);
plot(s2);

The unwrapping of the intensity of the spin-wave located around \([0,-1,1]\) Bragg peak shows:

MAPS Fe data; Spin-wave scattering intensity the the origin centred about the \([0,-1,1]\) Bragg peak. A visible gap caused by missing detectors is obvious in the \(\phi\)-axis range \([-50^\circ:+50^\circ]\). Inset: Linear projection of the same region; the red lines show the approximate mapping from the linear to spherical projections.

Integrating over the whole \(\theta\) range and thus including other detectors substantially improves statistics; this is done by setting the \(\theta\) parameter to [0, 180]:

s2 = cut(data_source, sp_proj, [0, 0.1, 2], [0, 180], [-180, 4, 180], [50, 60]);

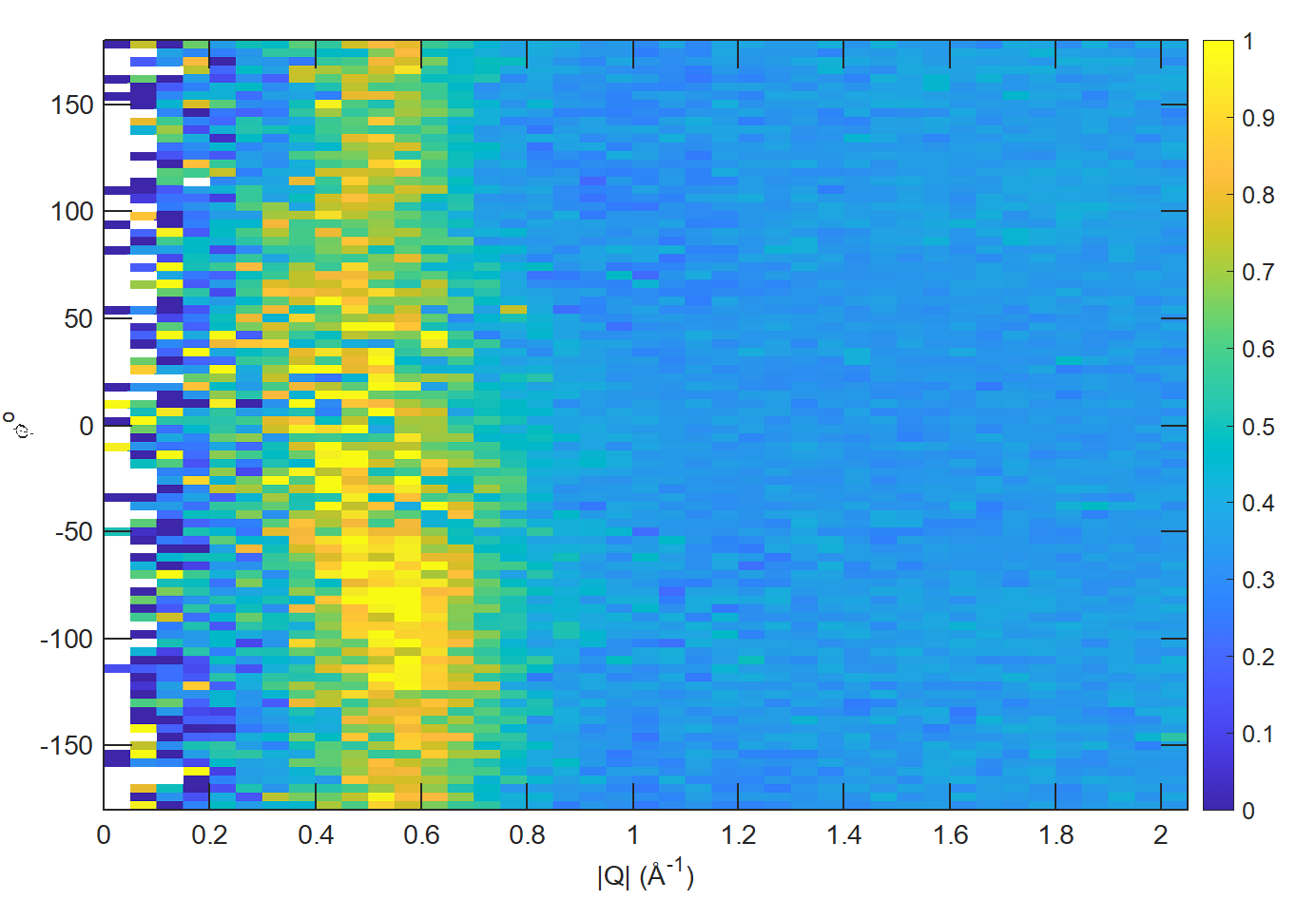
MAPS Fe data; Scattering intensity from cut averaged over all \(\theta\) spin-wave with the origin centred at the \([0,-1,1]\) Bragg peak.

The 1D cut below, generated by further integrating over the \(\phi\)-axis, shows the intensity distribution as a function of \(|\textbf{Q}|\), i.e. the distance from the spin-wave centre:

s2 = cut(data_source, sp_proj, [0, 0.1, 2], [0, 180], [-180, 180], [50, 60]);

Scattering intensity as function of distance from the scattering centre at \([0,-1,1]\).

5.1.5.3. Cylindrical Projections

In order to construct a cylindrical projection (i.e. a projection in \(\vec{Q}_{\perp}\) (the radial distance from the polar axis), \(\vec{Q}_{\|}\) (distance from origin along the polar axis), \(\phi\) (azimuthal angle) and \(E\)) coordinate system we create a projection in a similar way to the line_proj, but use the cylinder_proj class.

The complete signature for cylinder_proj is:

proj = cylinder_proj([u][, v][, type][, alatt][, angdeg][, offset][, label][, title][, lab1][, lab2][, lab3][, lab4])

where:

• u The vector \(\vec{u}\) is the reciprocal space vector defining the polar-axis of the cylindrical coordinate system along which \(\vec{Q}_{\|}\) is measured.

  See the diagram below for details.

• v The vector \(\vec{v}\) is the reciprocal space vector which defines the second component of the \(u\)-\(v\) plane from which \(\phi\) is measured.

  See the diagram below for details.

Note

The reciprocal space vectors \(u\)-\(v\) are not necessarily orthogonal so the actual axis from which \(\phi\) is measured lies in the plane defined by \(u\)-\(v\) vectors, orthogonal to \(u\).

Note

By default a cylinder_proj will define its principal axes \(u\) and \(v\) along the \(hkl\) directions \([1,0,0]\) and \([0,1,0]\) respectively.

• type Three character string denoting the the projection normalization of each dimension, one character for each directions, e.g. 'aad' or 'aar'.

  Similarly to sphere_proj there are 6 possible options for scaling momentum transfer components (\(Q_{\perp}\) and \(Q_{\|}\)) of type(1) and type(2) values:

  1. 'a' correspondent \(|Q|\)-component is measured in inverse angstroms.

  2. 'r' Reciprocal lattice units (r.l.u.) which normalises vector’s component so that the scale is the maximal value of the projection of vector \(\vec{u}\) for \(Q_{\|}\) or vector \(\vec{v}\) for \(Q_{\perp}\) to the unit vectors directed along the reciprocal lattice vectors.

  3. 'p' The scale is the length of the vector \(\vec{u}\) for \(Q_{\perp}\) or \(\vec{v}\) for \(Q_{\|}\) vectors.

  4. 'h' The scale is the length of \(a^{*}\), the first vector of reciprocal lattice.

  5. 'k' The scale is the length of \(b^{*}\), the second vector of reciprocal lattice.

  6. 'l' The scale is the length of \(c^{*}\), the third vector of reciprocal lattice.

  There are 2 possible options for the third (angular) component of type:

  1. 'd' Degrees

  2. 'r' Radians

  For example, if we wanted the length components to be in inverse angstroms and the angles in degrees we would have type = 'aad'.

• alatt 3-vector of lattice parameters.

• angdeg 3-vector of lattice angles in degrees.

Note

In general, you should not need to define alatt or angdeg; by default they will be taken from the sqw object during a cut. However, there are cases where a projection object may need to be reused elsewhere.

• offset 3-vector in \((h,k,l)\) or 4-vector in \((h,k,l,e)\) defining the origin of the projection coordinate system.

• label, etc.

  See other plot arguments above.

Note

If you do not provide any arguments to cylinder_proj, by default it will build a cylinder_proj with u=[1,0,0], v=[0,1,0], type='ppd' and offset=[0,0,0,0].

cyl_pr = cylinder_proj()

cyl_pr =
   cylinder_proj with properties:
          u: [1 0 0]
          v: [0 1 0]
       type: 'ppd'
      alatt: []
     angdeg: []
     offset: [0 0 0 0]
      label: {'\Q_{\perp}'  '\Q_{||}'  '\phi'  'En'}
      title: ''

Note

Like line_proj, cylinder_proj can be defined using positional or keyword arguments. However the same recommendation applies that positionals should only be used to define u and v.

A cylinder_proj defines a coordinate system which represents the momentum transfer vector \(\vec{Q}\) in cylindrical coordinates. offset defines the zero point of the coordinate system. If offset is zero, \(\vec{Q}\) is the vector of momentum transfer from the neutron to the magnetic or phononic excitations as measured in the experiment. The energy transfer coordinate for cylinder_proj is the same as in linear coordinates.

As we do for spherical projections, we introduce an auxiliary orthogonal coordinate system where: the basis vector \(\vec{e_z}\) is a unit vector parallel to \(\vec{u}\) and the basis vector \(\vec{e_x}\) is orthogonal to \(\vec{e_z}\) and lies in the plane defined by \(\vec{u}\) and \(\vec{v}\) (see cylindrical coordinates below).

Note

When the crystal lattice is orthogonal, the vector \(\vec{e_z}\) is parallel to \(\vec{u}\) and vector \(\vec{e_x}\) is parallel to \(\vec{v}\).

cylinder_proj defines a cylindrical coordinate system, where:

• \({Q_\perp}=|\vec{Q}-\vec{e_z}(\vec{e_z}\cdot \vec{Q})|\) – The length of the orthogonal to axis \(\vec{e_z}\) part of the momentum transfer \(\vec{Q}\) measured from the cylinder_proj origin (offset) in \(hkl\).

• \(Q_{\|}\) – The length of the projection of the momentum transfer \(\vec{Q}\) measured from the cylinder_proj origin (offset) in \(hkl\) to \(\vec{e_z}\) axis of the cylinder_proj

• \(\phi\) – The angle measured between the vector \(\vec{Q_\perp}\) to the plane \(\vec{u}\)-\(\vec{v}\) , i.e. \(0^{\circ}\) lies in the \(\vec{u}\)-\(\vec{v}\) plane and \(90^{\circ}\) is normal to \(\vec{u}\)-\(\vec{v}\) plane (i.e. parallel to \(\vec{e_y}\)).

• \(E\) – The energy transfer as defined in line_proj

Note

\(\phi\) lies in the range between \(-180^{\circ}\) and \(180^{\circ}\). When the third component of type is r, these ranges are the equivalent in radians.

Cylindrical coordinate system used by cylinder_proj

Similarly to Spherical coordinate system used by sphere_proj, detailed description of the cylindrical coordinate system used by Horace together with the image of the used coordinate system are provided on MATLAB “cart2pol/pol2cart” help pages, as Horace uses these methods to convert array of vectors expressed in Cartesian coordinate system to cylindrical coordinate system and backward.

When it comes to cutting and plotting, we can use a cylinder_proj in exactly the same way as we would a line_proj, but with one key difference. The binning arguments of cut no longer refer to \(h,k,l,E\), but to \(Q_{\perp}\) (Q_tr), \(Q_{\|}\), \(\phi\) (phi), \(E\) variables.

sp_cut = cut(w, cylinder_proj, Q_tr, Q_||, phi, e, ...);

Warning

The form of the arguments to cut is still the same (see: Binning arguments). However:

• \(Q_{\perp}\) (Q_tr) runs from \([0, \infty)\)

• \(\phi\) runs between \([-180, 180]\).

Requesting binning outsize of these ranges will fail.

5.1.5.3.1. cylinder_proj 2D and 1D cuts examples:

Cylindrical projection can be used to obtain cylindrical cuts in a manner analogous to linear and spherical projections.

The main use of cylindrical projection is for cuts with axis parallel to the incident beam as background scattering in inelastic instruments often has cylindrical symmetry.

Taking the previously used dataset and using the code:

data_source = 'Fe_ei401.sqw';
cyl_proj = cylinder_proj('type','aad');

%% A

w2_Qtr_dE = cut(data_source, cyl_proj, [0, 0.1, 14], [-4, 4], [-180, 180], [-10, 4, 400]);
plot(w2_Qtr_dE);
keep_figure;

%% B

w2_Qtr_Qll = cut(data_source, cyl_proj, [0, 0.1, 14], [-4,0.1,4], [-180, 180], [50, 60]);
plot(w2_Qtr_Qll);
keep_figure;

%% C

w2_Qtr_phi = cut(data_source, cyl_proj, [0, 0.1, 14], [-4,,4], [-180,2,180], [50, 60]);
plot(w2_Qtr_phi);

one can easily obtain various cuts taken along different coordinate axes.

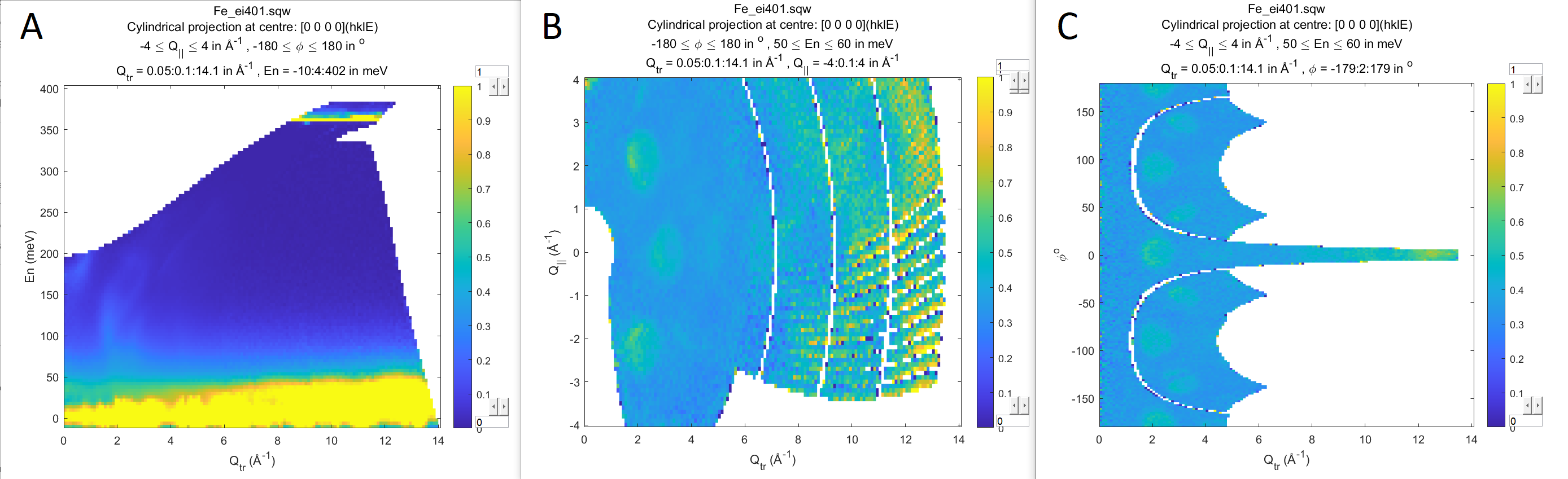
Cylindrical cuts along different coordinate axes

It is also possible to make one dimensional cylindrical cuts. The following code creates a plot which shows the behaviour of the scattering intensity as a function of \(Q_{\perp}\) at different \(Q_{||}\):

data_source ='Fe_ei401.sqw';
cyl_proj = cylinder_proj('type','aad');
n_cuts = 2;
w1 = repmat(sqw,1,n_cuts);
colors = 'krgb';
symbols = '.+*x';
for i=1:n_cuts
    cut_center = -4+(i-1)*(8/n_cuts);
    Qll_range = [cut_center-0.1,cut_center+0.1];
    w1(i) = cut(data_source, cyl_proj, [0, 0.1, 14], Qll_range, [-180,180], [50,60],'-nopix');
    acolor(colors(i));
    amark(symbols(i));
    pd(w1(i))
end
legend('Q_{\|}=-4','Q_{\|}=-2');

Cylindrical cuts along \(Q_{\perp}\)

5.1.6. Additional notes

Note

The number of binning arguments need only match the dimensionality of the object w (i.e. the number of plot axes), so can be fewer than 4.

Note

You cannot change the binning in a dnd object, i.e. you can only set the integration ranges, and have to use [] for the plot axis. The only option you have is to change the range of the plot axis by specifying [lo1,0,hi1] instead of [] (the ‘0’ means ‘use existing bin size’).

5.1.6.1. Auto-binning algorithm

When a cut will change projections (i.e. the source projection type is different or the principal-axes are not orthogonal to the target projection) there are a few things to be aware of, particularly when you specify automatic ([], [step]) binning arguments.

Binning range meaning

When you specify the binning ranges these are defined in the the “target” (desired) coordinate system. E.g. in cutting from a linear to a spherical projection, the meanings are:

x = sqw(..) % in linear projection
y = cut(x, sphere_proj(), **R**, **THETA**, **PHI**, **E**, ..)

Automatic Binning Arguments

If you provide automatic binning arguments, an algorithm will attempt to create the minimum bounding shape in the new projection that entirely encapsulates the source data. The parameters from this bounding shape will then be substituted into the places where automatic binning arguments are requested.

Warning

This algorithm will not change the number of bins unless the [step] form is used, but will change the ranges and thus the size of the bins in this instance.

If you do not specify a step, ensure you have checked that the binning is suitable in the new projection, or you may waste time having to re-cut your dataset.

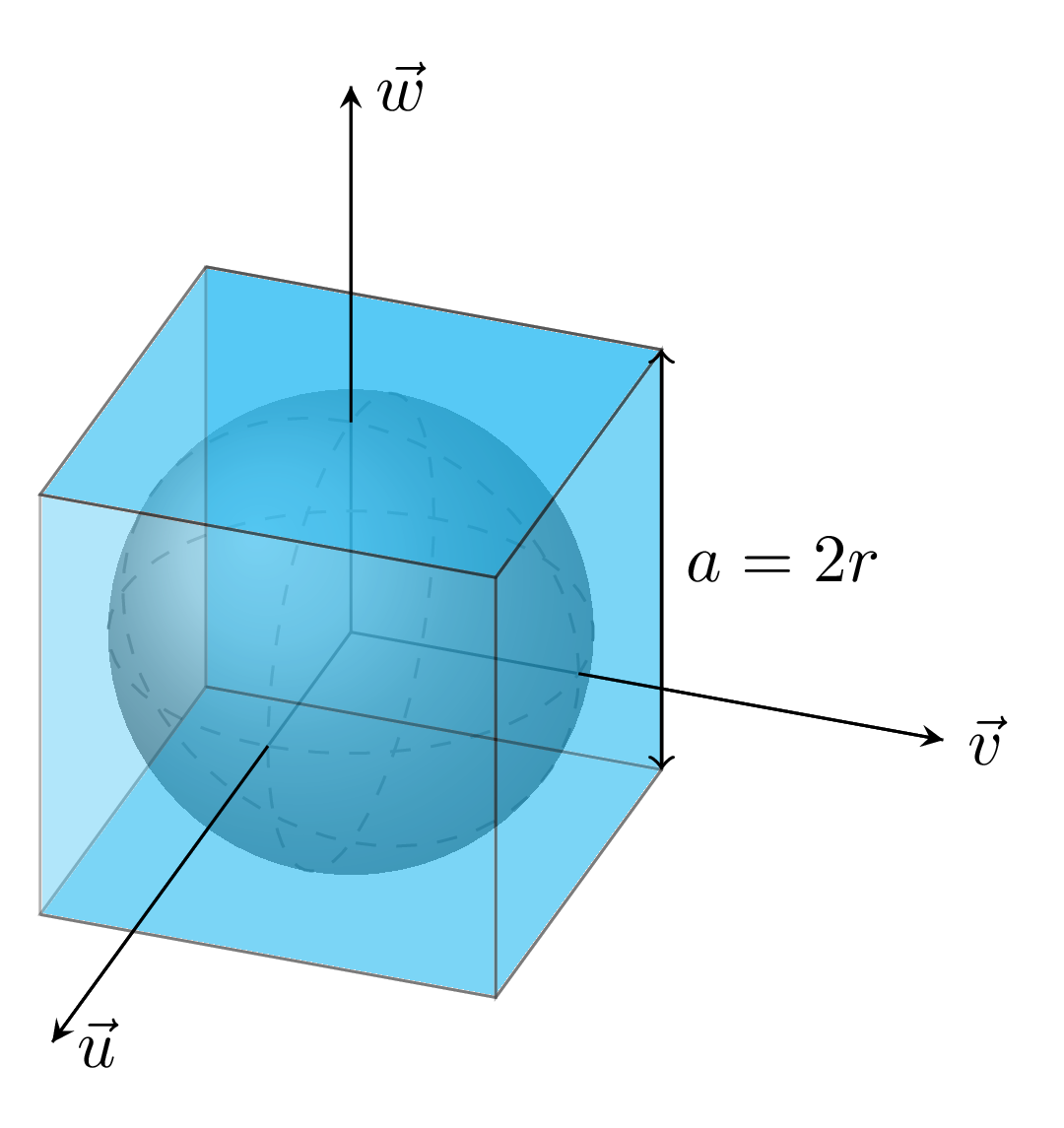
Example showing a linear projection (target) encapsulating a spherical projection (source). Here, if we consider a sphere of radius \(r\), then the encapsulating cuboid has sidelength (\(a\)) of size \(2r\).

Example

If:

• you provide an empty binning range ([]) as the third binning argument in your cut and,

• your source coordinate system is linear and,

• the target coordinate system is cylindrical, then:

the cut algorithm will try to compute the \(\phi\) range (the 3^rd coordinate of the cylindrical projection) which encapsulates the source cuboid in the target (cylindrical) coordinate system.

The number of bins in \(\phi\) will be equal to the number of bins in the 3^rd dimension (\(\vec{w}\)) of the source projection. If the 3^rd dimension of the source projection was an integration axis, the \(\phi\) of the target projection will also be an integration axis; if it was a plot axis, it will likewise remain a plot axis in the target projection, as expected.

Warning

In contrast to cutting without a projection change, when changing projections [] and [0] may behave differently.

• [] takes the number of bins in the source dimension

• [0] takes the step length in the source dimension

Without projection change this always produces reasonable result, but change in projection applies these values to different coordinate set.

Cutting with [0] may lead to strange or incorrect results when changing projections. E.g. a q-step of 0.01 may be reasonable in a linear projection, but when transformed to a spherical or cylindrical projection it may be used as the step size for the \(\phi\) binning range (-180:180 ), creating 36000 bins in \(\phi\) direction, which may be problematic.

Warning

The algorithm which identifies binning ranges is just a simple algorithm.

While it works reliably in simple cases, e.g. for transformations described by projections of the same kind (e.g. sphere_proj->sphere_proj), where the offset between the two projections is unchanged. In more complex cases (e.g. line_proj->cylinder_proj or where the polar-axis of the cylindrical projection is not aligned with any of the line_proj axes), the algorithm may not converge quickly. After a number of failed iterations, it will give up and issue a warning which looks like:

' target range search algorithm have not converged after 5 iterations.
  Search have identified the following default range:
 0        0.0120  -179.9641
 1.5843   90.0000  179.9641
 This range may be inaccurate'

Here, the first line shows the estimated lower bound and the second the estimated upper bound.

The user must evaluate how acceptable this result is for the desired cut and if in doubt, specify the binning arguments manually to get their desired binning.

5.1.7. Legacy calls to cut: cut_sqw and cut_dnd

Historically, cut came in two different forms cut_sqw and cut_dnd. These forms are still available now, however their uses are more limited and mostly discouraged.

• cut_sqw is fully equivalent to cut except that attempting to apply it to a dnd object or file, will raise an error.

• cut_dnd is equivalent to cut on a dnd object, but for an sqw object, it operates on the dnd (binned image) of the sqw, ignoring any pixel information and returning a dnd.

5.2. section

section is an sqw method, which works like cut, but uses the existing bins of an sqw object rather than rebinning.

wout = section(w, p1_bin, p2_bin, p3_bin, p4_bin)

Because it only extracts existing bins (and their pixels), this means that it doesn’t need to recompute any statistics related to the object itself and is therefore faster and more efficient. However, it has the limitation that it cannot alter the projection or binning widths from the original.

The parameters of section are as follows:

• w

  The array of sqw object(s) to be sectioned.

• pN_bin

  The range of bins specified as bin edges to extract from w.

  There are three valid forms for any pN_bin:

  • [], [0]

    Use the original binning.

  • [lo, hi]

    Take a section of original axis which lies between lo and hi values. The range of the resulting image in this case is the range between left edge of image bin containing lo value and right edge of bin containing hi value.

Note

The size of pN_bin must match the dimensionality of the underlying dnd object.

Note

These parameters are specified by inclusive edge limits. Any ranges beyond the the sqw object’s img_range will be reduced to only capture existing bins.

Warning

The bins selected will be those whose bin centres lie within the range lo - hi, this means that the actual returned img_range may not match [lo hi]. For example, a bin from 0 - 1 (centre 0.5) will be included by the following section despite the bin not being entirely contained within the range. The resulting image range will be [0 1].

section(w, [0.4 1])

In order to extract bins whose centres lie in the range [-5 5] from a 4-D sqw object:

w4_red = section(w4, [-5 5], [], [], [])