dnd vs sqw: the difference

This tutorial was originally a script designed to illustrate and explain the different key data types – sqw and dnd (the d0d, ``d1d`, … family). – in Horace, and why they are important.

Whole script available here.

The key difference is that sqw objects contain the exact data for each measurement (pixels) while dnd objects simply contain the histogrammed (binned) accumulation of these data.

For more information on the differences between dnd and sqw, see here.

%Take two cuts:
sqw_file='/mnt/data/Science/URu2Si2/data/sqw/Ei81_20K.sqw';

proj = line_proj([1, 0, 0], [0, 1, 0]);

csqw=cut(sqw_file, proj, [-0.5, 0.5], [-4, 0.04, -2], [-0.05, 0.05], [0, 0.8, 60]);

%identical to above, except extra argument at the end
cdnd=cut(sqw_file, proj, [-0.5, 0.5], [-4, 0.04, -2], [-0.05, 0.05], [0, 0.8, 60], '-nopix');

plot(compact(csqw));
lz 0 10;
keep_figure;

plot(compact(cdnd));
lz 0 10;
keep_figure;

Taking cut from data in file /mnt/data/Science/URu2Si2/data/sqw/Ei81_20K.sqw...
Step 1 of 1; Have read data for 5579774 pixels -- now processing data... -----> retained 1121852 pixels
Taking cut from data in file /mnt/data/Science/URu2Si2/data/sqw/Ei81_20K.sqw...
Step 1 of 1; Have read data for 5579774 pixels -- now processing data... -----> retained 1121852 pixels

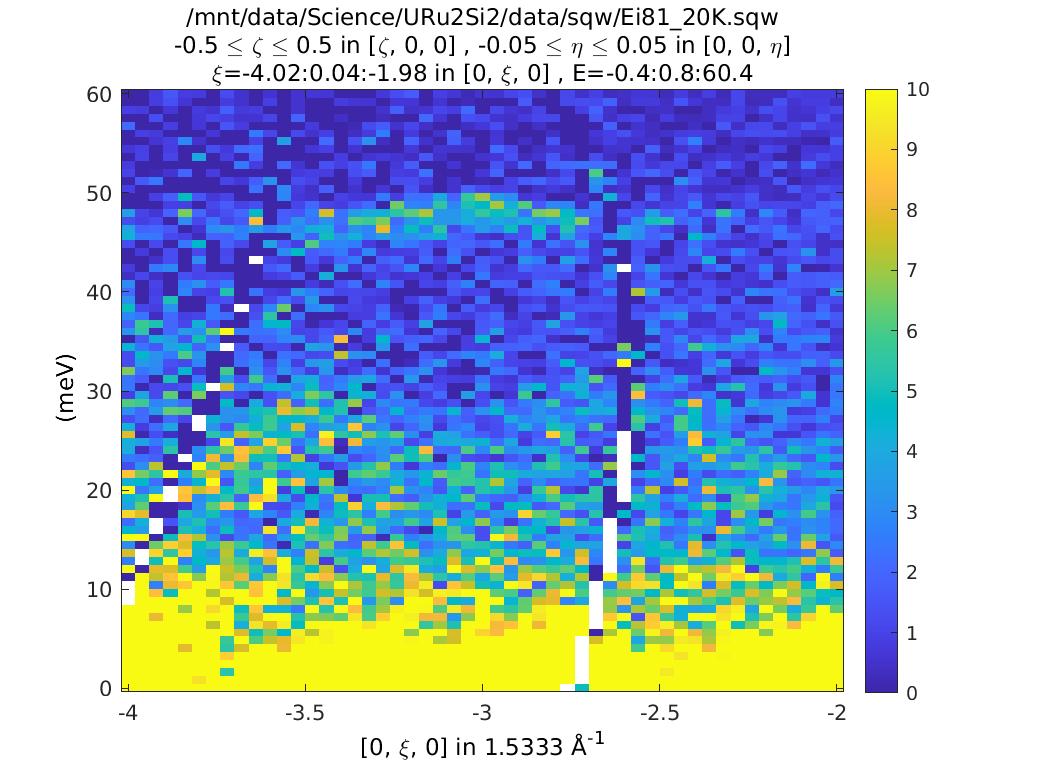
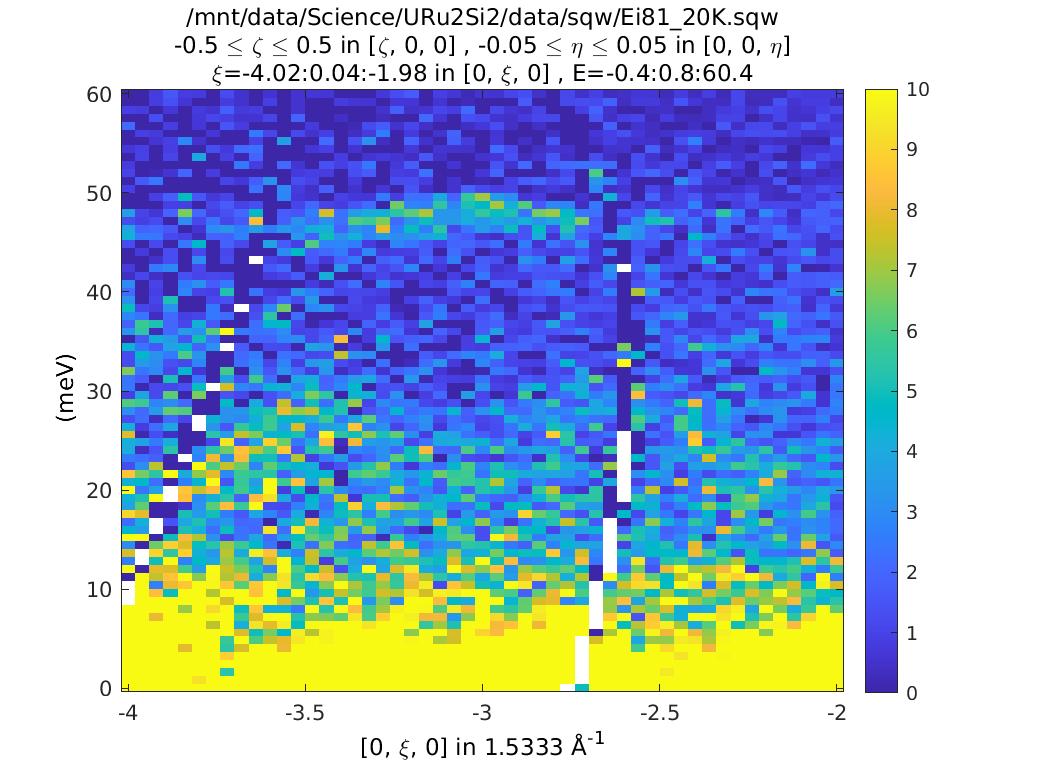
The plots look (are!) identical. So what’s the difference? Double click on them in the Workspace part of the Matlab window. You can see that the csqw object has a lot more information associated with it.

General principle

Use dnd if you are just looking at the data - it takes up less computer memory, which is a good thing.

If you want to fit or simulate the data and you are only simulating a basic function (i.e. using func_eval, multifit_func, etc) that does not depend on all 4 coordinates of Q and E, then use a dnd.

Example:

cgaussdnd=func_eval(cdnd, @gauss2d, [1, -3, 30, 0.2, 0.1, 100]);
plot(cgaussdnd);
keep_figure;

cgausssqw=func_eval(csqw, @gauss2d, [1, -3, 30, 0.2, 0.1, 100]);
plot(cgausssqw);
keep_figure;

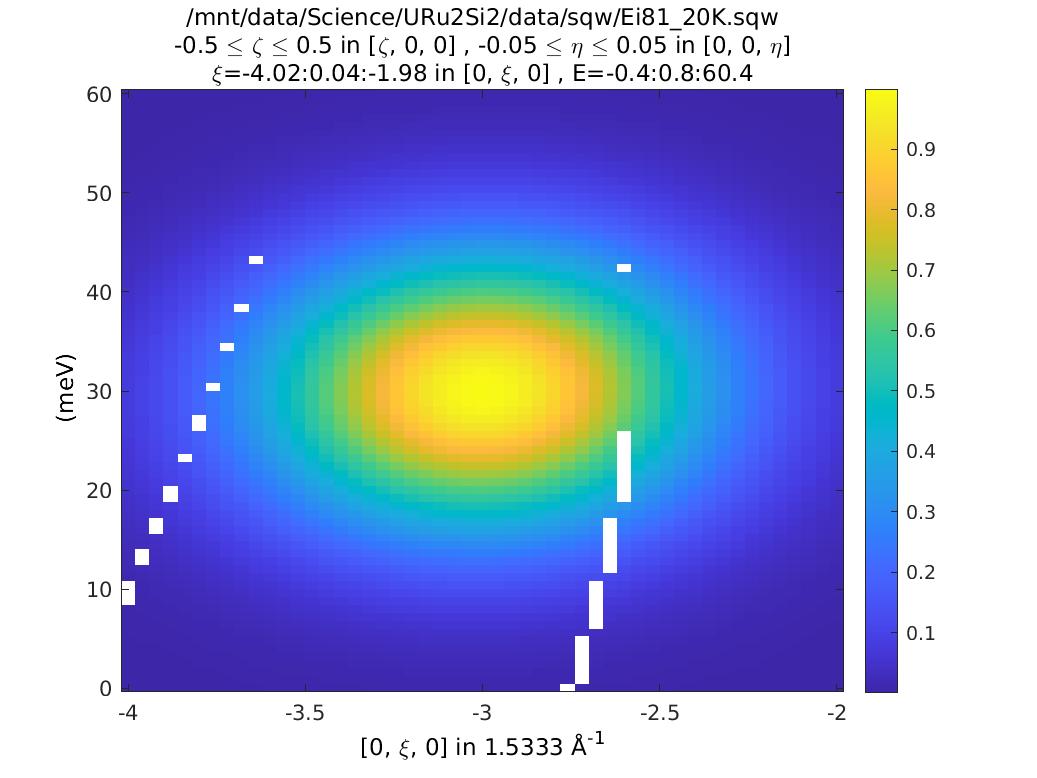
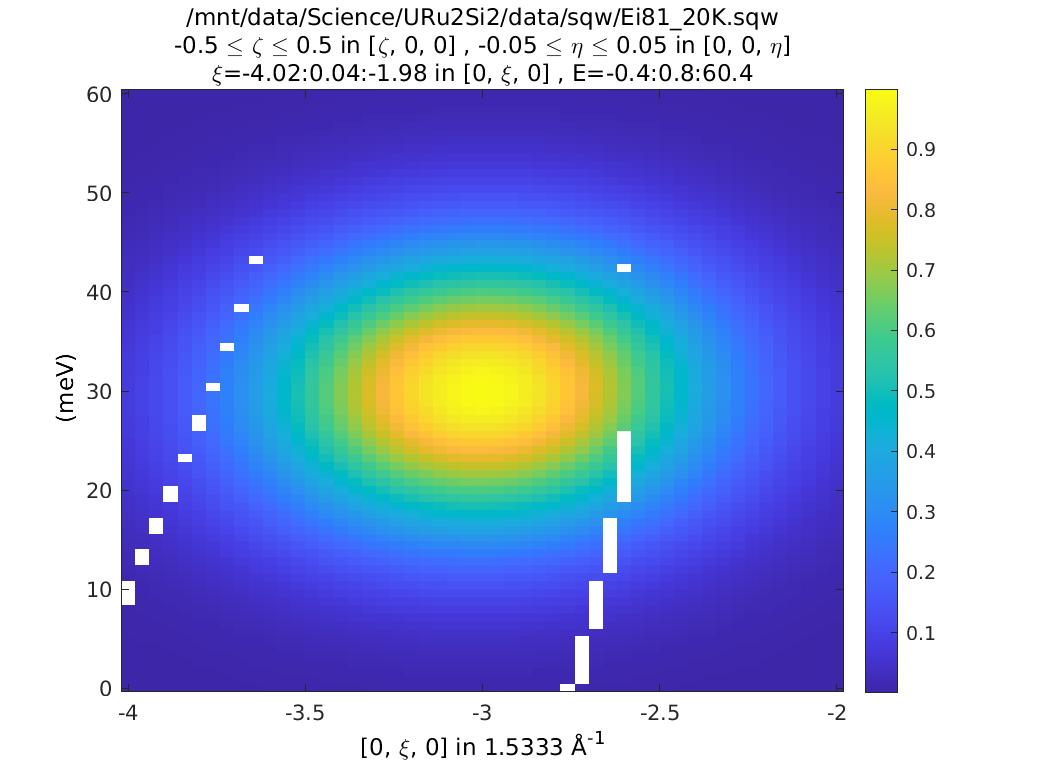
The two figures are identical, because the func_eval routine only uses the plot axis coordinates as its input, not (H, K, L, E).

If you want to fit or simulate data with an S(Q, E) model, you should use sqw. This is because you will account for the fact that you had to integrate along the non-plot axes correctly. The following example illustrates why this is important:

%model of ferromagnetic spin waves in the Horace demo
csimsqw=sqw_eval(csqw, @demo_FM_spinwaves_2dSlice_sqw, [4, 2, 1, 1, 1]);
csimdnd=sqw_eval(cdnd, @demo_FM_spinwaves_2dSlice_sqw, [4, 2, 1, 1, 1]);

%Dispersion has equal steepness along all reciprocal space directions.
plot(csimsqw);
keep_figure;

plot(csimdnd);
keep_figure;

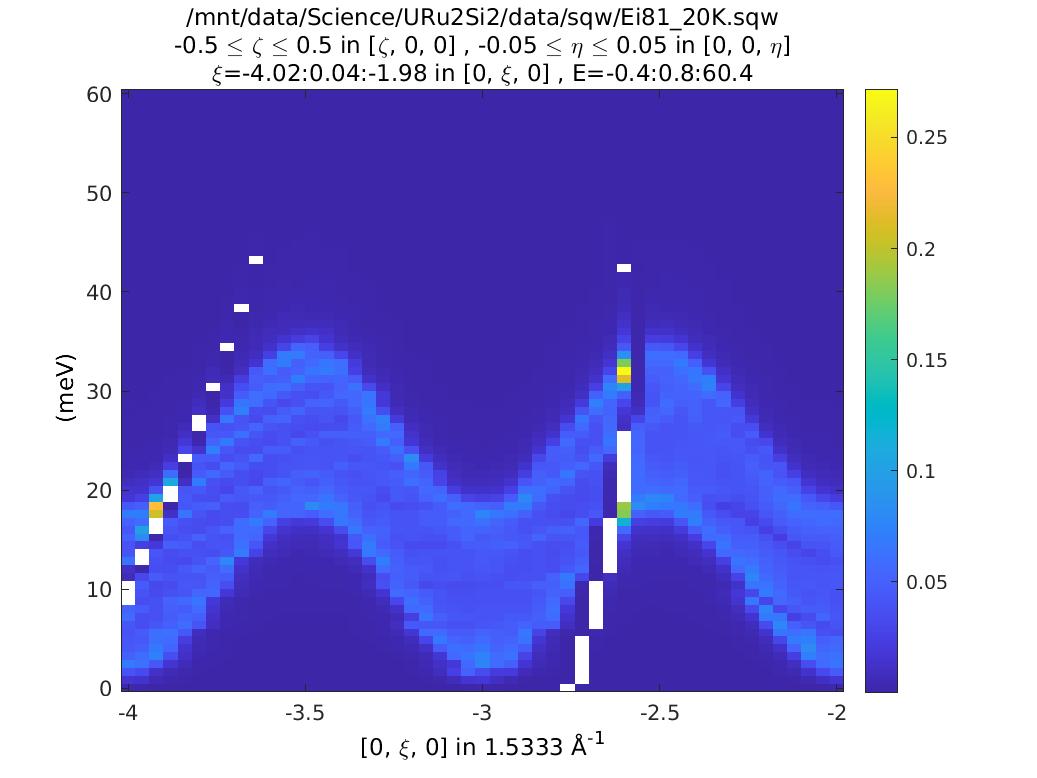
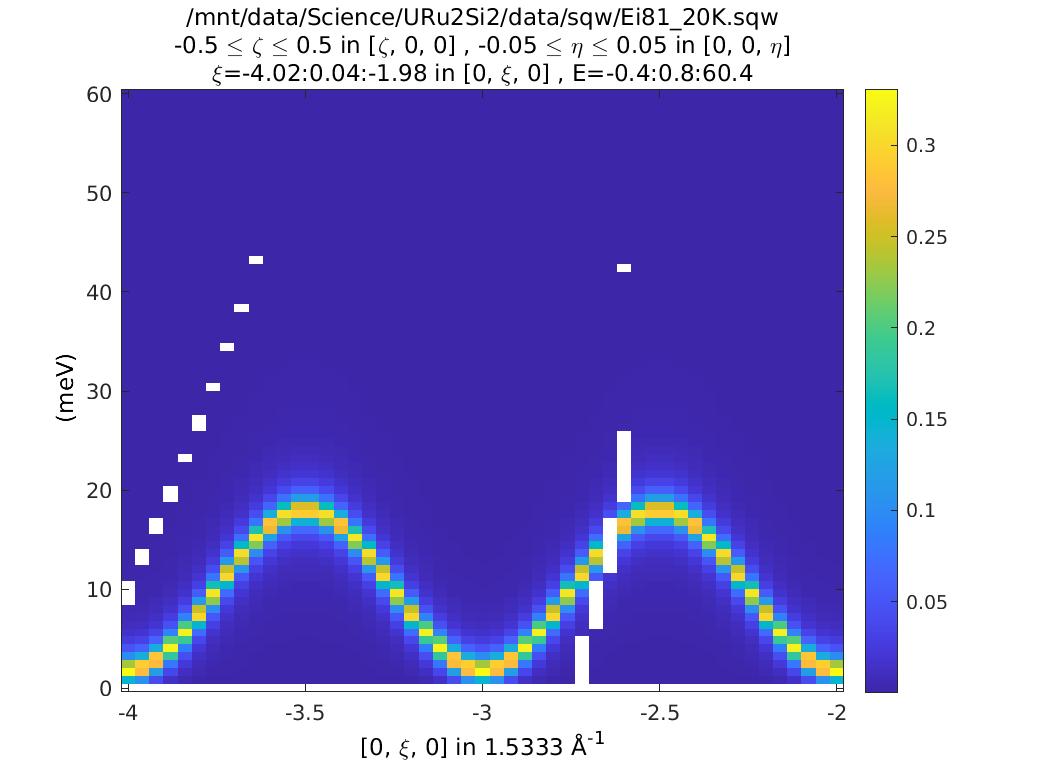
These are totally different.

Why?

Because the simulation of the sqw object includes the dispersion along the H-axis, and calculates what it is for the pixels actually measured. The simulation of the dnd object assumes that every point has the average value of H (zero in this case). So the latter gives a sharp dispersion, whereas the former is very broad.

So if you have data from a system where there is some variation in the signal along a non-plot axis, you should use simulate with sqw objects in order to capture this correctly.

Specific case A: resolution modelling

If you want to include resolution in your simulation or fitting, you must use Tobyfit, and you also need the detector pixel information that you get in an sqw object but not in a dnd.

Warning

Tobyfit will give an error message if you try to use it with a dnd.

Specific case B: spurion identification

See separate tutorial about how to do this. Basically, if you need to know something about data from a particular run, or from a particular detector, you need sqw.

Specific case C: smoothing

If you apply the smooth algorithm to your data you will get a dataset of the same type back again. Smoothing works for dnd, but is forbidden for sqw data. The reason is that the smoothing operation only makes sense in the plot axis coordinate frame. But doing that means you lose the connection between the signal displayed in the plot and the detector pixel information that contributed to it.

Specific case D: symmetrisation

Warning

Currently in Horace 4.0.0, dnd symmetrisation is disabled. Due to extended transforms in the sqw object.

Symmetrisation does different things for sqw and dnd data. The latter can be folded along an axis parallel to a plot axis. The former can be folded along any axis. Generally you are much safer doing symmetrisation with sqw objects.

Whole Script

%Take two cuts:
sqw_file='/mnt/data/Science/URu2Si2/data/sqw/Ei81_20K.sqw';

proj = line_proj([1, 0, 0], [0, 1, 0]);

csqw=cut(sqw_file, proj, [-0.5, 0.5], [-4, 0.04, -2], [-0.05, 0.05], [0, 0.8, 60]);

%identical to above, except extra argument at the end
cdnd=cut(sqw_file, proj, [-0.5, 0.5], [-4, 0.04, -2], [-0.05, 0.05], [0, 0.8, 60], '-nopix');

plot(compact(csqw));
lz 0 10;
keep_figure;

plot(compact(cdnd));
lz 0 10;
keep_figure;

cgaussdnd=func_eval(cdnd, @gauss2d, [1, -3, 30, 0.2, 0.1, 100]);
plot(cgaussdnd);
keep_figure;

cgausssqw=func_eval(csqw, @gauss2d, [1, -3, 30, 0.2, 0.1, 100]);
plot(cgausssqw);
keep_figure;

%model of ferromagnetic spin waves in the Horace demo
csimsqw=sqw_eval(csqw, @demo_FM_spinwaves_2dSlice_sqw, [4, 2, 1, 1, 1]);
csimdnd=sqw_eval(cdnd, @demo_FM_spinwaves_2dSlice_sqw, [4, 2, 1, 1, 1]);

%Dispersion has equal steepness along all reciprocal space directions.
plot(csimsqw);
keep_figure;

plot(csimdnd);
keep_figure;